1)

\(\)Seema flies a kite on a 16 m string at an inclination of 60 degree. What is the height of the kite above the ground?

SSC CGL 2020

A)

\({4 \sqrt3} m\)

B)

\({16 \sqrt3} m\)

C)

\({6 \sqrt3} m\)

D)

\({8 \sqrt3} m\)

Correct Option: D

\({8 \sqrt3} m\)

---

\(sin60^o = {\sqrt3 \over2}={AB \over AC}\),

\(AB = 8\sqrt3 m\)

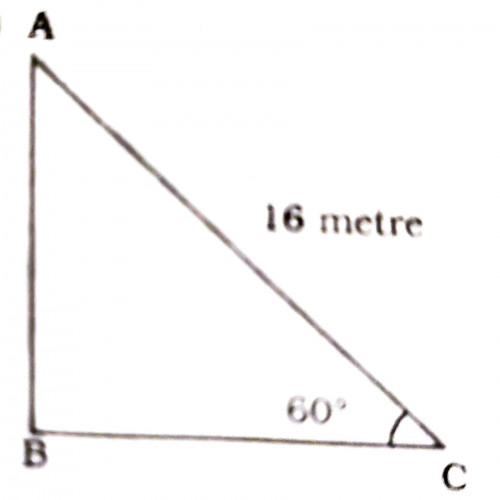
2)

From the top of a tower, the angles of depression of two objects on the ground on the same side of it, are observed to be \( 60^\circ and 30^\circ\) respectively and the distance between the objects is \(400 \sqrt3\) metre. The height (in metre) of the tower is:

SSC CGL 2019

A)

800

B)

\(800\sqrt3\)

C)

600

D)

\(600\sqrt3\)

Correct Option: C

600

---

BC = \(400 \sqrt3 \)m;
In \(\triangle ACD\),
tan \(60^0 = \frac{\sqrt{3}}{1} = \frac{AD}{CD}\);
In\( \triangle ABD\),
tan \(30^0 = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} = \frac{AD}{BD};\)
BC = BD - CD = 3 - 1 = 2 units;
2 units = 400 x
\(\sqrt{3} \)units =\( \frac{400 \sqrt3}{2} \times \sqrt{3}\) = 600 m

3)

P and Q are two points on the ground on either side of a pole. The angles of elevation of the top of the pole as observed from P and Q are \(60^0\) and \(30^0\), respectively and the distance between them is \(84\sqrt3\)m. What is the height (in m) of the pole?

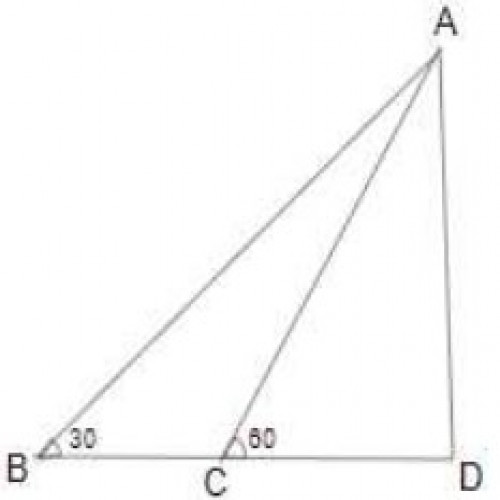
SSC CGL 2019

A)

63

B)

73.5

C)

52.5

D)

60

4)

From a point exactly midway between the foot of two towers P and Q,the angles of elevation of their tops are \(30^0\)and \(60^0\), respectively. The ratio of the height of P to that of Q is:

SSC CGL 2019

A)

1 : 3

B)

1 : 2

C)

\(1:2\sqrt3\)

D)

\(2 : 3\sqrt3\)

Correct Option: A

1 : 3

---

\(tan 30 = {1\over \sqrt{3}} = {P\over x}\)   ;

  \(tan 60 = { \sqrt{3}} = {Q\over x}\)

\({P\over Q} = {1\over 3}\)

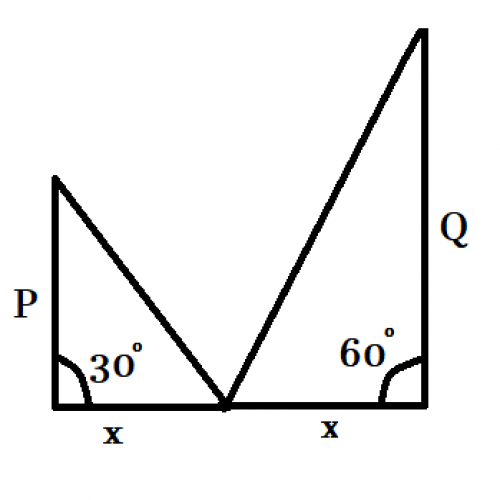
5)

The angle of elevation of the top of a pillar from the foot and the top of a building 20 m high, are 60° and 30° respectively. The height of the pillar is

SSC CGL 2016

A)

3 m

B)

9 m

C)

27 m

D)

30 m

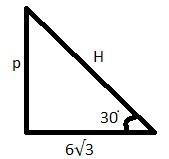
6)

A straight vertical pole was broken during a cyclone in such a way that its top touched the ground at a distance of  \(6\sqrt 3\)  m from the bottom of the pole and made and angle of 30° with the horizontal. What was the height (in m) of the pole?

SSC CHSL 2021

A)

12

B)

18

C)

\(12\sqrt 3\)

D)

\(18\sqrt 3\)

Correct Option: B

18

---

In fig, we have to calculate P + H

tan 30° = P/6√3, P = 6m

Also, sin 30° = P/H, we get H= 12m

thus, P + H = 18m

 

7)

A kite is flying at a height of 138 m above the ground. It is attached to a string inclined at 45° to the horizontal. What is the approximate length (in m) of the string?

SSC CHSL 2021

A)

193

B)

194

C)

190

D)

195

8)

The string of a kite is 158 m long and it makes an angle of 30° with the horizontal. What is the height (in m) of the kite ?
Assume there is no slack in the string.

SSC CHSL 2021

A)

99

B)

79

C)

100

D)

80

9)

As observed from the top of a lighthouse, 42 m high above sea-level, the angle of depression of a ship sailing directly towards it changes from 30° to 45°. The distance travelled by the ship during the period of observation is:

SSC CHSL 2021

A)

\(42(\sqrt 3 - 1)\)

B)

\(42(\sqrt 3 + 1)\)

C)

42

D)

\(42(1 - \sqrt 3 )\)

10)

The angle of elevation of a ladder against a wall is 45°. The length of the ladder is 12 m. What is the distance between the wall and the foot of the ladder?

SSC CHSL 2021

A)

\(6\sqrt 2 \ m\)

B)

\(3\sqrt 2 \ m\)

C)

\(5\sqrt 3 \ m\)

D)

\(4\sqrt 3 \ m\)