1)

The graphs of the equations 3x + y - 5 = 0 and 2x - y - 5 = 0 intersect at the point P(\({\alpha,\beta}\)). What is the value of (\({3\alpha+\beta}\)) ?

SSC CGL 2019

A)

4

B)

-4

C)

3

D)

5

2)

The graph of the equation x - 7y = -42, intersects the y-axis at \(P\left(\alpha,\beta\right)\) and the graph of 6x + y - 15 = 0, intersects the x-axis at \( Q\left(\gamma,\delta\right)\) , What is the value of \(\alpha+\beta+\gamma+\delta\)?

SSC CGL 2019

A)

\(17\over2\)

B)

6

C)

\(9\over2\)

D)

5

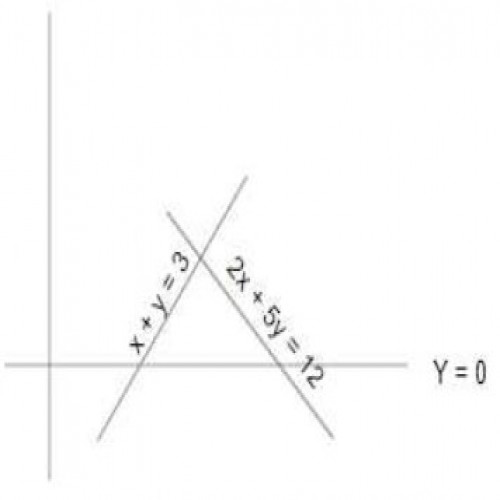
3)

What is the area (in square units) of the triangular region enclosed by the graphs of the equations x + y = 3, 2x + 5y= 12 and the x-axis?

SSC CGL 2019

A)

2

B)

3

C)

4

D)

6

Correct Option: B

3

---

x + y = 3;
2x + 2y = 6 ---(1);
2x + 5y = 12 ---(2);
From eq (1) and eq (2), 3y = 6; y=2; so height = 2; put the value of y in eq(1) and (2), x = 3; and x = 6;  Area = \({1\over2}\times base\times height\)= \({1\over2}\times(6-3)\times2=3\) square units

4)

The graph of the equations 5x - 2y + 1 = 0 and 4y - 3x +5 = 0 , intersect at the point P (\(\alpha, \beta\) ). What is the value of \((2\alpha - 3\beta)\)?

SSC CGL 2019

A)

4

B)

6

C)

-4

D)

-3

5)

The point of intersection of the graphs of the equations 3x - 5y = 19 and 3y - 7x + 1 =0 is P\((\alpha,\beta)\) . What is the value of \((3\alpha-\beta)\)?

SSC CGL 2019

A)

-2

B)

-1

C)

1

D)

0

6)

The graphs of the equations 2x+3y=11 and x-2y+12=0 intersects at P (\(x_1,y_1\)) and the graph of the equations x-2y+12=0 intersects the x-axis at \(Q(x_2,y_2)\). What is the value of \((x_1-x_2+y_1+y_2)\)?

SSC CGL 2019

A)

13

B)

-11

C)

15

D)

-9