objective Ques (161 results)
1)In the given fig. triangle ABC, \(\theta = 80^o\) the measure of each of the other two angle will be:
SSC CGL 2020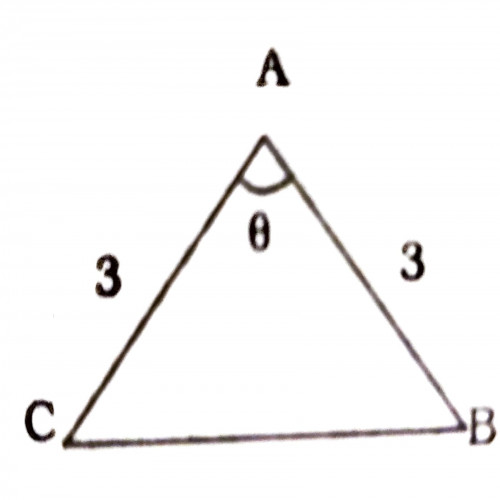
\(50^0\)
since the two sides are equal in length, and equal side corresponds equal angle, therefore \(2x + \theta = 180\), x = 50
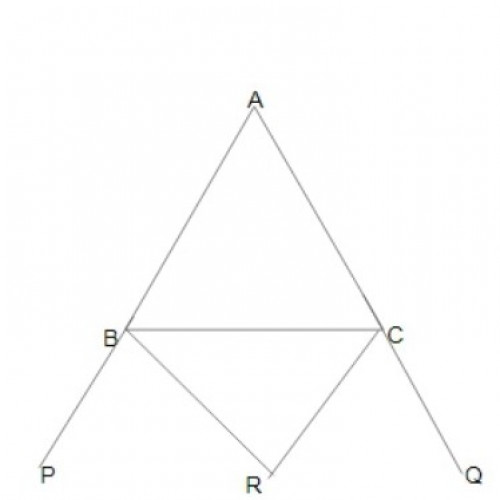
SSC CGL 20192)The sides AB and AC of \( {\Delta ABC}\) are produced to P and Q resepectively. The bisectors of \({\angle CBP}\) and\({\angle BCQ}\) meet at R. If the measure of \({\angle A}\) is 44º, then what is the measure of \({1\over2 }\)\({\angle BRC}\)?
34º
\(\angle BRC = 90 ^o - \angle A/2; = 90 ^o - 44^o/2 = 90 ^o - 22^o = 68^o; \frac{1}{2} \angle BOC = \frac{68^o}{2}; \frac{1}{2} \angle BOC = 34^o;\)
SSC CGL 20193)In \( {\Delta ABC}\), D is a point on side BC such that \({\angle ADC}={\angle BAC}\). If CA = 12cm, CB = 8cm, then CD is equal to :
18 cm.
\(\angle ADC = \angle BAC; \angle ACB = \angle ACD; So, \triangle ABC ~ \triangle DCA,; So, \frac{BC}{AC} = \frac{AC}{CD}; \frac{8}{12} = \frac{12}{CD};\)
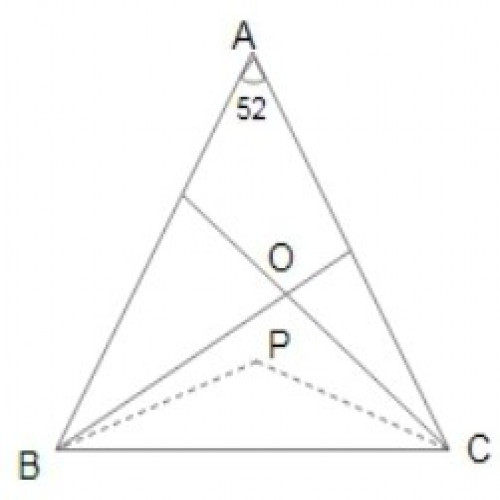
SSC CGL 20194)In \({\Delta ABC}, \angle A =52^0\) and O is the orthocentre of the triangle (BO and CO meet AC and AB at E and F respectively when produced). If the bisectors of \({\angle OBC} \) and \({\angle OCB}\) meet at P, then the measure of \({\angle BPC}\) is :
154º
By the orthogonal property,
\(\angle BOC = 180 - \angle A\);
\(\angle OBC + \angle OCB = \angle A;\)
\(\angle BPC = 180 - \angle A/2;\)
\(\angle BPC = 180 - \angle 52/2 = 180 - 26 = 154^0\)
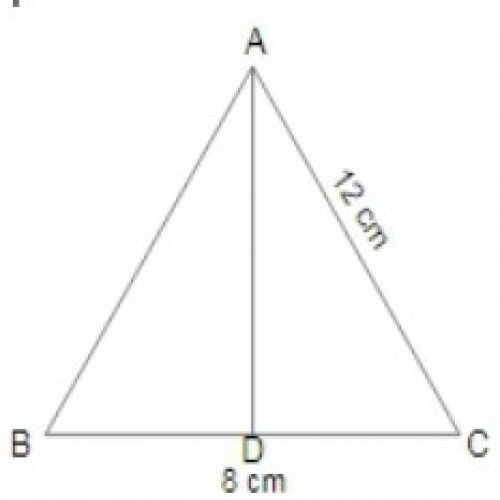
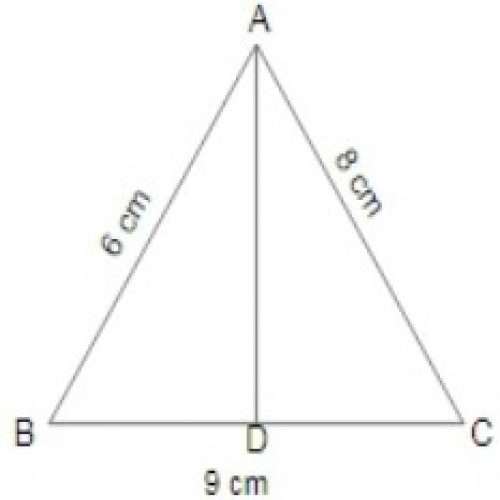
SSC CGL 20195)In \(\Delta ABC\), AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is :
\({\sqrt{119}\over 2}\) cm
In ΔABC, AD is median . D. will be the mid point of BC.
BD = CD = BC/2= 9/2 = 4.5 cm;
\(AB^2 + AC^2 = 2(AD^2 + BD^2);\)
\(6^2 + 8^2 = 2(AD^2 + (4.5)^2);\)
\(100/2 = AD^2 + 20.25\);
\(AD^2 = 29.75 = 119/4;\)
\(AD = \frac{\sqrt{119}}{2}\)
SSC CGL 20196)In \( \triangle ABC\), AB=7cm, BC=10cm, and AC = 8 cm. If AD is the angle bisector of \(\angle BAC\), where D is a point on BC, then BD is equal to:
\({14 \over3}cm\)
Let the BD = x,
DC = 10 - x
By angle bisector theorem,
\(\frac{BD}{CD}\) =\( \frac{AB}{AC} \); \(\frac{x}{10 - x}\) = \(\frac{7}{8}\)
8x = 70 - 7x
15x = 70
x = 14/3 cm
BD = \(\frac{14}{3}\)
SSC CGL 20197)The sides of a triangle are 11 cm, 60 cm and 61 cm. What is the radius of the circle circumscribing the triangle?
30.5 cm
Radius of the circle circumference = hypotenuse/2 = 61/2 = 30.5 cm
SSC CGL 20198)In\( \triangle ABC\),\( \angle A = 58^\circ.\) If I is the in center of the triangle, then the measure of \(\angle BIC\) is:
\(119^0\)
\(\angle BIC = 90^0 + \angle A/2\);
\(\angle BIC = 90^0+ 58/2 = 90^0 + 29^0 = 119^0\)
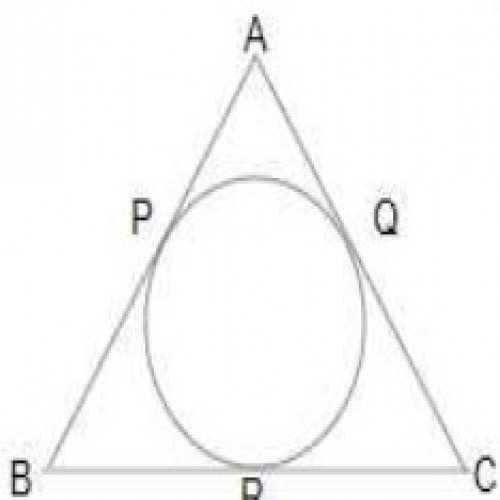
SSC CGL 20199)A circle is inscribed in \( \triangle ABC\) , touching AB, BC and AC at the points P, Q and R respectively. If AB - BC = 4 cm, AB - AC = 2 cm and the perimeter of \(\triangle ABC\) = 32 cm, then PB + AR is equal to:
\(38\over3\) cm
Perimeter = 32 cm;
AB + BC + AC = 32 cm ---(1);
AB - BC = 4 cm ---(2);
AB - AC = 2 cm ---(3);
On eq(1) + (2) + (3),
3AB = 38;
AB = PB + AR = 38/3
SSC CGL 201910)The sides of a triangle are 12 cm, 35 cm and 37 cm. What is the circumradius of the traingle?
18.5 cm.