objective Ques (45 results)
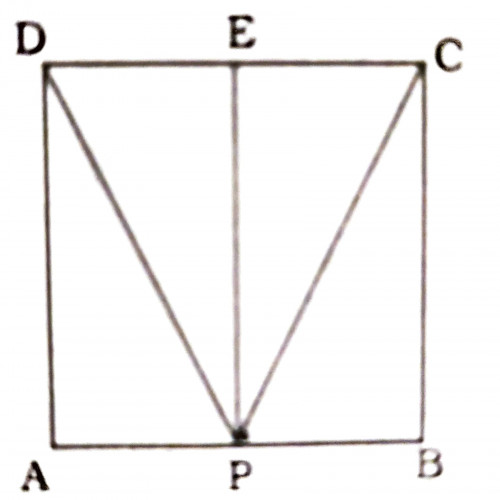
SSC CGL 20201)Triangle PDC is drawn inside the square ABCD of side 24cm where P lies on AB. What is the area of the triangle ?
288\(cm^2\)
since ABCD is a square, Area of triangle PDC = \( {1 \over 2}\times CD \times PE\) = \( {1 \over 2}\times 24 \times 24 = 288 cm^2\)
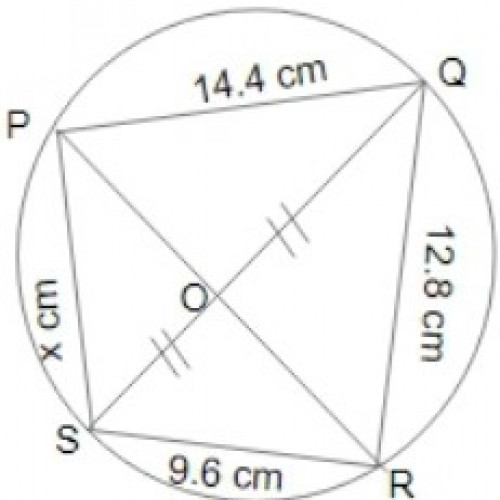
SSC CGL 20192)PQRS is a cyclic quadrilateral in which PQ = 14.4 cm. QR = 12.8 cm and SR = 9.6 cm. If PR bisects QS, what is the length of PS?
19.2 cm
By the property,
\(PQ \times QR = RS \times PS\);
\(14.4 \times 12.8 = 9.6 \times x;\)
9.6x = 184.32;
x = 19.2 cm
SSC CGL 20193)If each interior angle of a regular polygon is \( \left(128\frac{4}{7}\right)^\circ\) , then what is the sum of the number of its diagonals and the number of its sides?
21
Interior angle = \(180 - \frac{360}{n}\);
\(128\frac{4}{7}^\circ = 180 - \frac{360}{n}\);
\(\frac{900}{7}^\circ = 180 - \frac{360}{n}\);
\( \frac{360}{n} = 180 - \frac{900}{7}\);
\( \frac{360}{n} = \frac{360}{7} \); Side(n) = 7;
Number of diagonals =\( \frac{n(n - 3)}{2} = \frac{7(7 - 3)}{2} = \frac{28}{2} = 14 \); Sum of the number of its diagonals and the number of its sides = 7 + 14 = 21
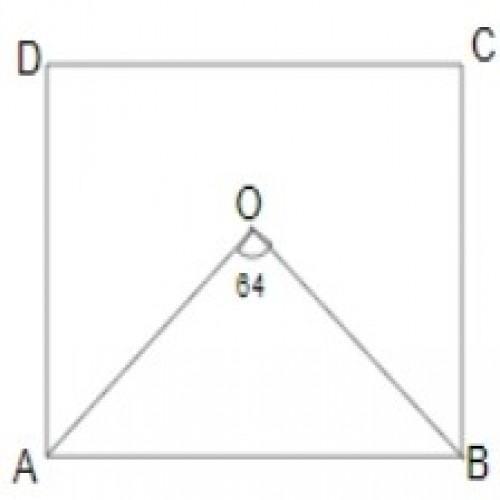
SSC CGL 20194)In quadrilateral ABCD, the bisectors of\( \angle A \)and \(\angle B\) meet at O and \(\angle AOB = 64^\circ\).\( \angle C + \angle D\) is equal to:
\(128^0\)
In \(\triangle AOB\),
\(\angle OAB + \angle OBA + \angle O = 180\);
\(\angle OAB + \angle OBA = 180 - 64 = 116^0\);
\(\angle OAB \)and\( \angle OBA \) is the bisector of\( \angle A and \angle B\).
So,
\(\angle A + \angle B = 2 \times 116 = 232^0;\)
\(\angle A + \angle B + \angle C + \angle D = 360;\)
\(\angle C + \angle D = 360 - 232 = 128^0\)
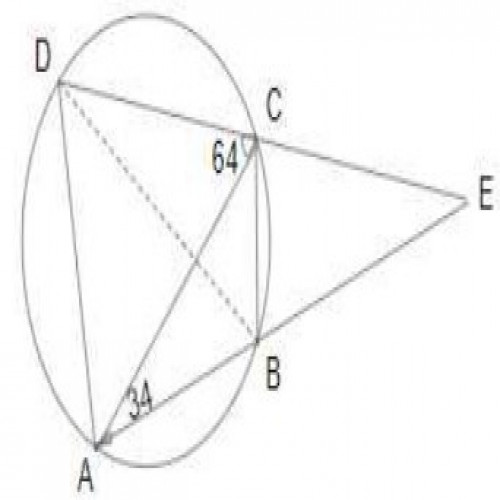
SSC CGL 20195)In a circle with centre O, ABCD is a cyclic quadrilateral and AC is the diameter. Chords AB and CD are produced to meet at E. If \(\angle CAE = 34^0\) and \(\angle E = 30^0\), then \(\angle CBD\) is equal to :
\(26^0\)
By the exterior angle property, \(\angle DCA=30 +34=64\); \(\angle DCA=180-90-64=26\); \(\angle DAC=\angle CBD\); \(\angle CBD=26^0\)
SSC CGL 20196)In quadrilateral ABCD, \(\angle C=72^0\) and \(\angle D = 28^0\). The bisectors of \(\angle A\) and \(\angle B\) meet at O. What is the measure of \(\angle AOB\)?
\(50^0\)
SSC CGL 20197)If the measure of each exterior angle of a regular polygon is \((51\frac{3}{7})^0\), then the ratio of the number of its diagonals to the number of its sides is:
2 : 1
As we know,
Number of sides in the polygon = 360/exterior angle = \({360 \over 51\frac{3}{7}^0} = 7\)
Number of diagonal = [n (n – 3)]/2 = [7 (7 – 3)]/2 = [7 × 4]/2 =14
Required ratio = 14 : 7 = 2 : 1
SSC CGL 20198)The sum of the interior angles of a regular polygon is \(1260^0\). What is the difference between an exterior angle and an interior angle of the polygon?
\(100^0\)
SSC CGL 20199)In a quadrilateral ABCD, the bisectors of \(\angle C\) and \(\angle D\) meet at E. If \(\angle CED=56^0\) and \(\angle A = 49^0\), then the measure of \(\angle B\) is:
\(63^0\)
SSC CGL 201910)A circle is inscribed in a quadrilateral ABCD touching AB, BC, CD and AD at the points P, Q, R and S, respectively, and \(\angle B=90^0\). If AD = 24 cm, AB = 27 cm and DR = 6 cm, then what is the circumference of the circle?
\(18\pi cm.\)